| 47 |
Set Theory |
| What is Musical Set Theory? |
||||||
After Brahms, tonality in Western music began to break down. Whereas before composers had relied upon a specific key area to organize the notes they wrote (e.g. a concerto in C-Sharp Minor). The idea of having such a tonal “home-base” had grown stale by the turn of the 20th century. Composers needed a new system to organize their pitches. Arnold Schoenberg spearheaded the move away from tonality and began writing atonal music around 1908. By 1923, he had fully developed a “12-tone” system of pitch organization, in which the composer arranges all twelve unique pitches into an ordered row and performs various manipulations on that row to generate pitch content for a composition. This system is usually referred to as ‘serialism.’ Set theory is not the same as serialism, but the two share many of the same methods and ideas. Set theory encompasses the notion of defining sets of pitches and organizing music around those sets and their various manipulations. Set class analysis refers to the efforts of music theorists to reveal the systems that composers like Schoenberg and his followers used to organize the pitch content of their works. Keep in mind that sets and set classes determined pitch content only; the composers remained free to fashion all other aspects of the music according to their artistic desires (at least until super-serialism, a philosophy of subjecting every aspect of the music to serial techniques, came into fashion in the 1950s). In their day, Mozart, Haydn, and Beethoven were collectively referred to as “The Viennese School” of composers. Schoenberg’s ideas about music were so unorthodox and so radically changed the face of music history, that together with two of his students from Vienna, Alban Berg and Anton Webern, they are called “The Second Viennese School.” |
|||||
| What is a Pitch Class Set? |
||||||
A Pitch Class Set is simply an unordered collection of pitches. The 12 unique pitches on the keyboard, or pitch classes, are numbered from 0 to 11, starting with ‘C’. For example, the pitch class set consisting of the notes C, E, and G would be written as (047). It is a common practice to use the letters T and E for the numbers 10 and 11 to avoid confusion when noting sets. It also eliminates the need to use commas between the numbers. Set class (016) was so popular with Schoenberg and his disciples that it has been nicknamed “The Viennese Trichord.” |
|||||
| What does it mean to invert a set? |
||||||
| A melody is inverted by swapping the direction of its intervals. If the original goes up a minor third, the inversion goes down a minor third. In set theory, any note can be inverted by subtracting its value from 12. (The inversion of 1 is 11, the inversion of 2 is 10, etc. 0 and 6 invert onto themselves.) If you map a set onto a clockface, the inversion of that set is its mirror image on the clock. The axis of inversion lies on the line between the 0 and the 6 on the clockface, so when you invert a set it looks like it was flipped horizontally. |
|||||
| What is Normal Form? |
||||||
| Pitch sets can be put into Normal Form, which is an ordering of the pitches in the set which is deemed the most “compact.” Compact ordering means that the largest of the intervals between any two consecutive pitches is between the first and last pitch listed. If you look at a pitch set graphed on a clock face, the normal form will be the clockwise spelling of the set that traverses the smallest distance on the circumference of the circle. The set (2,9,10), for example, is not in normal form because the interval between 2 and 9 (7) is larger than the intervals between 9 and 10 (1) or between 10 and 2 (4). To put the set (2,9,10) into normal form, you would spell it (9,10,2). That way the largest interval is “on the outside.” If there is no single interval that is larger than all the others, then the normal form is the representation of the set that is “packed most tightly to the left,” that is, the representation where smaller intervals are closer to the beginning of the set and larger intervals are nearer to the end. For example, (0,2,3,7) is packed more tightly to the left than (0,4,5,7) because the largest interval on the inside of (0,2,3,7) is between the 3 and the 7 (or “to the right”), whereas the largest interval on the inside of (0,4,5,7) is between the 0 and the 4, closer to the left. Both of these sets are in normal form, but the first is “packed more tightly to the left.” |
|||||
| What is Prime Form? |
||||||
| If you obtain the normal form of a set and the normal form of its inversion, then its prime form would be the more tightly packed of the two normal forms, transposed to begin on zero. For example, consider the set (7,8,2,5), which we’ll call set A. Here is how we would calculate its prime form: 1. The normal form of A is (2,5,7,8). 2. The inversion of A is (5,4,10,7). 3. The normal form of A inverted is (4,5,7,10). 4. Since (4,5,7,10) is packed more tightly to the left than (2,5,7,8), we transpose (4,5,7,10) to begin on zero and get (0,1,3,6) as the prime form. Why is this useful? Prime form is an abstraction of set classes that gives a unique “picture” of that particular collection of notes. If two sets have the same prime form, we can be assured that they will sound similar to one another. Sets with the same prime form contain the same number of pitches and the same collection of intervals between its pitches, hence they are in some sense aurally “equivalent,” in much the same way that all major chords are aurally equivalent in tonal music. Prime form representations are also referred to as “Set classes.” Sets whose prime forms are identical are said to belong to the same set class. For example, the pitch class sets (127), (823), and (0E6) all belong to set class (016). |
|||||
| What is a Forte Number? |
||||||
| Allen Forte, perhaps the most important music theorist of our time, catalogued every possible prime form for sets with 3-9 members and ordered them according to their interval content. He gave each of these prime forms a name, like “5-35.” The first number is an index of how many pitches are in the set, the second number was assigned by Dr. Forte. The complement of a set consists of all notes not in the set. Complement sets share the same catalog number in Forte’s classification system (e.g., the complement of 5-35 is 7-35). Here is a brief list of just a few popular forte numbers: 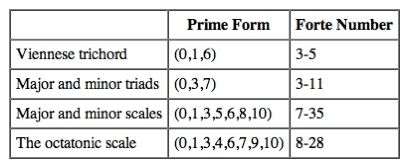 Allen Forte is on the music faculty at Yale University. He introduced this system of numbering the prime forms in his 1977 book titled The Structure of Atonal Music. |
|||||